Kaip sėkmingai išspręsti “Futoshiki” galvosūkius

Šioje pamokoje žingsnis po žingsnio pateikiami pagrindiniai ir pažangūs “Futoshiki” galvosūkių sprendimo būdai su pridedamomis iliustracijomis, parodančiomis metodus konkrečiose lentų konfigūracijose.

Išeities taškas, norint pasiekti sprendimą, yra paties žaidimo apibrėžimas: “Futoshiki” reikalauja, kad vartotojas sužinotų lentą, kurioje kiekvienas skaitmuo rodomas vieną kartą kiekvienoje eilutėje ir stulpelyje, gerbiant lentų nelygybę. Naudojant šį kriterijų, pažanga siekiant sprendimo gali būti padaryta žingsnis po žingsnio užpildant tuščius lentų kvadratus su konkrečiais skaitmenimis, nes jie yra vienintelis būdas laikytis lentų apribojimų.

Stulpelių ir eilučių išimtys

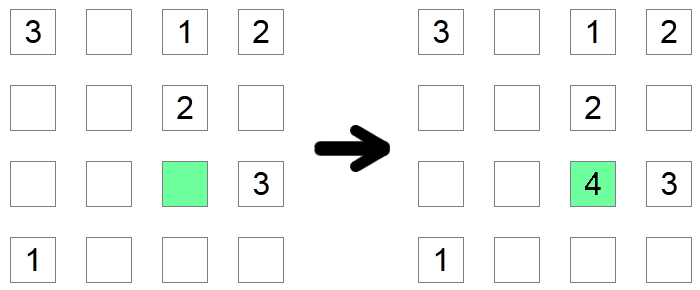
Jei kvadratų stulpelyje ir eilutėje jau yra visi galimi skaitmenys, išskyrus vieną, tada tame kvadratėlyje turi būti trūkstamas skaitmuo. Aukščiau pateiktame pavyzdyje žalias kvadratas turi būti 4, nes neleidžiama turėti jokios kitos vertės, nes kiti galimi skaitmenys jau yra jo eilutėje ar stulpelyje.

Nelygybių grandinė

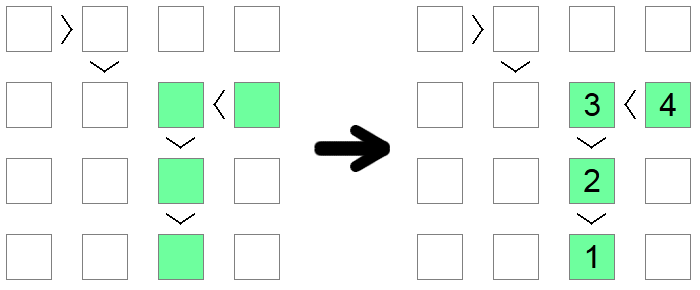
Jei pastebite nelygybių grandinę, ar tai būtų arba < (visos didėjančios), ar > (visos mažėjančios), vienodo dydžio su lentų dydžiu, tai ta grandinė turi būti seka nuo 1 iki lentos ilgio. Grandinės ilgis garantuoja, kad ši seka yra vienintelis galimas sprendimas, tenkinantis nelygybės grandinės primetamą monotono sąlygą.

Priverstinės minimalios ir maksimalios vertės

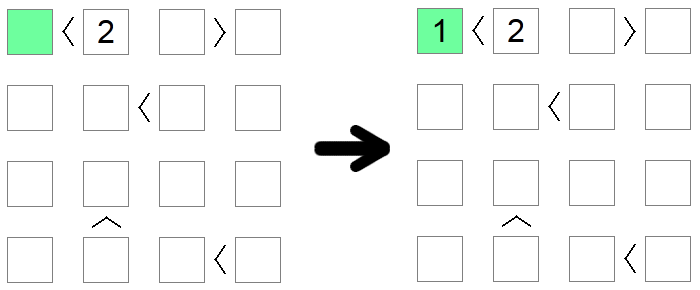
Kvadratai, kurie yra mažesni nei 2, netiesiogiai turi turėti vertę 1, nes tai yra vienintelė leistina vertė lentoje, kuri atitinka šią sąlygą. Panašiai kvadratai, kurie yra didesni už lentos dydį minus 1, turi būti lygūs lentos dydžiui. Aukščiau pateiktame pavyzdyje vienintelė galima žaliojo kvadrato vertė (mažesnė nei 2) yra 1.

Min. ir maksimalių verčių išskyrimas

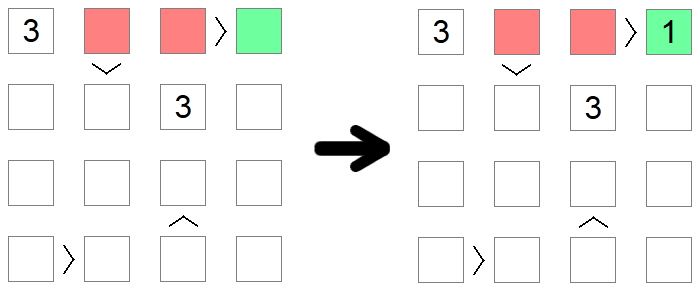
Kvadratai, kurie yra didesni už kitus kvadratus, negali būti 1, mažiausia leistina vertė lentoje, nes nėra vertės, mažesnės nei 1. Panašiai kvadratuose, kurie yra mažesni už kitus kvadratus, negali būti max leistinos reikšmės, nes kitoje nelygybės pusėje nebūtų nieko didesnio, kurį būtų galima užpildyti. Aukščiau pateiktame pavyzdyje 1 negalima užpildyti raudonais kvadratais, nes jie visi yra didesni už kitus lentos kvadratus, todėl vienintelis galimas 1 vieta pirmoje lentos eilėje yra žalias kvadratas.

Taisyklių derinimas

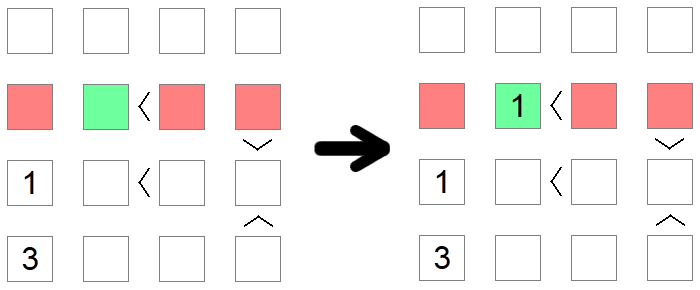
Kartais norint padaryti išvadą, reikia naudoti kelias taisykles. Taip yra aukščiau pateiktame pavyzdyje, kur mes bandome įdėti vertę 1 antroje lentos eilutėje. Pirmasis raudonas kvadratas pašalinamas dėl stulpelio išskyrimo (tame stulpelyje jau turime 1), o antrasis ir trečiasis raudoni kvadratai pašalinami dėl minimalių reikšmių išskyrimo, nes tose vietose yra didesnė nei su jomis susijusi nelygybė. Todėl žalias kvadratas išlieka vienintele galima vieta 1 patalpinti toje eilėje.

Pakartotinių galimybių

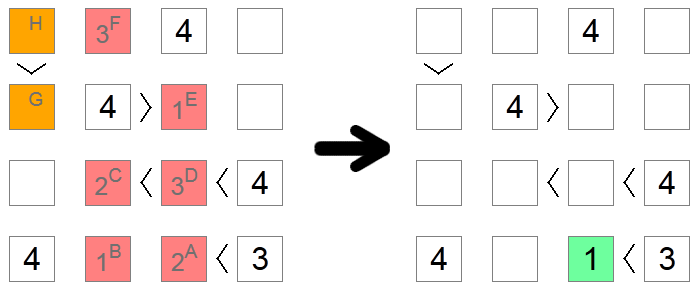
Kartais, ypač sunkiose lentose, nėra kitų būdų išsiaiškinti teisingą kvadrato skaitmenį, išskyrus pasinerimą į kiekvienos galimybės pasekmes, kol nepasiekiamas prieštaravimas. Aukščiau pateiktame pavyzdyje visi raudoni ir oranžiniai kvadratai iš pradžių yra tušti. Mes norime išsiaiškinti, ar kvadratas A yra 1 ar 2. Darome prielaidą, kad jame yra 2, ir patikriname, ar mes pasiekiame prieštaravimą, pagrįstą šia prielaida.

Jei kvadratas A turi 2, tada kvadratas B turėtų 1 (vienintelė likusi vertė apatinėje eilutėje). Kvadratas C gali būti 1 arba 2, nes jame yra nelygybių grandinė, dėl kurios reikia turėti 2 didesnius skaičius, tačiau dabar jis negali būti 1 dėl stulpelio išskyrimo kvadrato B, taigi kvadratas C yra 2, o kvadratas D yra 3 (vienintelė reikšmė tarp 2 ir 4). Dėl stulpelių išimčių kvadratas E yra 1, o kvadratas F yra 3.

Dabar, jei pažvelgtume į oranžinius kvadratus, pastebime prieštaravimą: jei kvadratas G būtų 2, kvadratas H turėtų būti arba 3, arba 4, kurie neleidžiami dėl eilutės išskyrimo. Jei kvadratas G būtų 3, kvadratas H turėtų būti 4, o tai neleidžiama dėl tos pačios priežasties. Kadangi nebeturime likusių kvadrato G reikšmių, tai reiškia, kad pasiekėme aklavietę ir mūsų pradinė prielaida buvo klaidinga: 2 nėra tinkamas žingsnis kvadratui A, todėl galime eiti į priekį ir jame pastatyti 1, vienintelę kitą galimą vertę.

Išvados

Aukščiau parodėme, kaip sėkmingai išspręsti “Futoshiki” galvosūkį, apimant įvairius metodus, kurie gali padėti jums nustatyti kitą žingsnį net sudėtingose situacijose. Kitas pagrindinis ingredientas, padedantis tapti įgudusiam ir greitam “Futoshiki” galvosūkių sprendimui, yra patirtis: kuo daugiau praktikuosite, tuo geresni ir greitesni tapsite.

Jei youre up už iššūkį, galite žaisti dabar atsitiktinį Futoshiki galvosūkį paspaudę mygtuką žemiau. Sėkmės!

Žaisk “Futoshiki”